Ley de tensión de Kirchhoff

Esta ley es llamada también segunda ley de Kirchhoff, ley de lazos de Kirchhoff o ley de mallas de Kirchhoff (es común que se use la sigla LVK para referirse a esta ley).
                         

                                                   

En un lazo cerrado, la suma de todas las caídas de tensión es igual a la tensión total suministrada. De forma equivalente, la suma algebraica de las diferencias de potencial eléctrico en un lazo es igual a cero.

${\displaystyle \sum _{k=1}^{n}V_{k}=V_{1}+V_{2}+V_{3}\dots +V_{n}=0}$

De igual manera que con la corriente, las tensiones también pueden ser complejos, así:

${\displaystyle \sum _{k=1}^{n}{\tilde {V}}_{k}=0}$

Esta ley se basa en la conservación de un campo potencial de energía. Dado una diferencia de potencial, una carga que ha completado un lazo cerrado no gana o pierde energía al regresar al potencial inicial.

Esta ley es cierta incluso cuando hay resistencia en el circuito. La validez de esta ley puede explicarse al considerar que una carga no regresa a su punto de partida, debido a la disipación de energía. Una carga simplemente terminará en el terminal negativo, en vez del positivo. Esto significa que toda la energía dada por la diferencia de potencial ha sido completamente consumida por la resistencia, la cual la transformará en calor. Teóricamente, y, dado que las tensiones tienen un signo, esto se traduce con un signo positivo al recorrer un circuito desde un mayor potencial a otro menor, y al revés: con un signo negativo al recorrer un circuito desde un menor potencial a otro mayor.

En resumen, la ley de tensión de Kirchhoff no tiene nada que ver con la ganancia o pérdida de energía de los componentes electrónicos (Resistores, capacitores, etc.). Es una ley que está relacionada con el campo potencial generado por fuentes de tensión. En este campo potencial, sin importar que componentes electrónicos estén presentes, la ganancia o pérdida de la energía dada por el campo potencial debe ser cero cuando una carga completa un lazo.

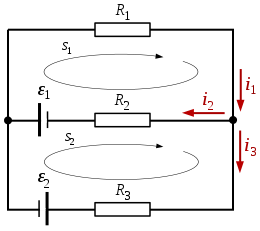
Asumiendo una red eléctrica consistente en dos fuentes y tres resistencias, disponemos la siguiente resolución: (antes de empezar, en necesario aclarar la convención de signos: si recorro la malla a favor de la corriente, el potencial asociado a la resistencia es negativo; caso contrario es positivo. Si recorro la fuente y hay una subida de potencial (de - a +), la fem es positiva; caso contrario es negativa).

De acuerdo con la primera ley de Kirchhoff (ley de los nodos), tenemos:

${\displaystyle i_{1}-i_{2}-i_{3}=0\,}$

La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s₁, nos hace obtener:

${\displaystyle -R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}=0}$

La segunda ley de Kirchhoff (ley de las mallas), aplicada a la malla según el circuito cerrado s₂, por su parte:

${\displaystyle -R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}=0}$

Debido a lo anterior, se nos plantea un sistema de ecuaciones con las incógnitas ${\displaystyle i_{1},i_{2},i_{3}}$:

${\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}&=0\\\end{cases}}}$

Dadas las magnitudes:

${\displaystyle R_{1}=100,\ R_{2}=200,\ R_{3}=300,\ \epsilon _{1}=3,\ \epsilon _{2}=4}$,

la solución definitiva sería:

${\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}\\i_{2}={\frac {4}{275}}\\i_{3}=-{\frac {3}{220}}\\\end{cases}}}$

Se puede observar que ${\displaystyle i_{3}}$ tiene signo negativo, lo cual significa que la dirección de ${\displaystyle i_{3}}$ es inversa respecto de lo que hemos asumido en un principio (la dirección de ${\displaystyle i_{3}}$ -en rojo- definida en la imagen).